A Likert scale (pronounced /ˈlɪkərt/,[1] also /ˈlaɪkərt/) is a psychometric scale commonly used in questionnaires, and is the most widely used scale in survey research, such that the term is often used interchangeably with rating scale even though the two are not synonymous. When responding to a Likert questionnaire item, respondents specify their level of agreement to a statement. The scale is named after its inventor, psychologist Rensis Likert.[2]
Sample question presented using a five-point Likert item
An important distinction must be made between a Likert scale and a Likert item. The Likert scale is the sum of responses on several Likert items. Because Likert items are often accompanied by a visual analog scale (e.g., a horizontal line, on which a subject indicates his or her response by circling or checking tick-marks), the items are sometimes called scales themselves. This is the source of much confusion; it is better, therefore, to reserve the term Likert scale to apply to the summated scale, and Likert item to refer to an individual item.
A Likert item is simply a statement which the respondent is asked to evaluate according to any kind of subjective or objective criteria; generally the level of agreement or disagreement is measured. Often five ordered response levels are used, although many psychometricians advocate using seven or nine levels; a recent empirical study[3] found that a 5- or 7- point scale may produce slightly higher mean scores relative to the highest possible attainable score, compared to those produced from a 10-point scale, and this difference was statistically significant. In terms of the other data characteristics, there was very little difference among the scale formats in terms of variation about the mean, skewness or kurtosis.
The format of a typical five-level Likert item is:
1. Strongly disagree
2. Disagree
3. Neither agree nor disagree
4. Agree
5. Strongly agree
Likert scaling is a bipolar scaling method, measuring either positive or negative response to a statement. Sometimes a four-point scale is used; this is a forced choice method[citation needed] since the middle option of "Neither agree nor disagree" is not available.
Likert scales may be subject to distortion from several causes. Respondents may avoid using extreme response categories (central tendency bias); agree with statements as presented (acquiescence bias); or try to portray themselves or their organization in a more favorable light (social desirability bias). Designing a scale with balanced keying (an equal number of positive and negative statements) can obviate the problem of acquiescence bias, since acquiescence on positively keyed items will balance acquiescence on negatively keyed items, but central tendency and social desirability are somewhat more problematic.
Scoring and analysis
After the questionnaire is completed, each item may be analyzed separately or in some cases item responses may be summed to create a score for a group of items. Hence, Likert scales are often called summative scales.
Whether individual Likert items can be considered as interval-level data, or whether they should be considered merely ordered-categorical data is the subject of disagreement. Many regard such items only as ordinal data, because, especially when using only five levels, one cannot assume that respondents perceive all pairs of adjacent levels as equidistant. On the other hand, often (as in the example above) the wording of response levels clearly implies a symmetry of response levels about a middle category; at the very least, such an item would fall between ordinal- and interval-level measurement; to treat it as merely ordinal would lose information. Further, if the item is accompanied by a visual analog scale, where equal spacing of response levels is clearly indicated, the argument for treating it as interval-level data is even stronger.
When treated as ordinal data, Likert responses can be collated into bar charts, central tendency summarised by the median or the mode (but some would say not the mean), dispersion summarised by the range across quartiles (but some would say not the standard deviation), or analyzed using non-parametric tests, e.g. chi-square test, Mann–Whitney test, Wilcoxon signed-rank test, or Kruskal–Wallis test.[4] Parametric analysis of ordinary averages of Likert scale data is also justifiable by the Central Limit Theorem, although some would disagree that ordinary averages should be used for Likert scale data.
Responses to several Likert questions may be summed, providing that all questions use the same Likert scale and that the scale is a defendable approximation to an interval scale, in which case they may be treated as interval data measuring a latent variable. If the summed responses fulfill these assumptions, parametric statistical tests such as the analysis of variance can be applied. These can be applied only when more than 5 Likert questions are summed.[citation needed]
Data from Likert scales are sometimes reduced to the nominal level by combining all agree and disagree responses into two categories of "accept" and "reject". The chi-square, Cochran Q, or McNemar test are common statistical procedures used after this transformation.
Consensus based assessment (CBA) can be used to create an objective standard for Likert scales in domains where no generally accepted standard or objective standard exists. Consensus based assessment (CBA) can be used to refine or even validate generally accepted standards.
Level of measurement
The five response categories are often believed to represent an Interval level of measurement. But this can only be the case if the intervals between the scale points correspond to empirical observations in a metric sense. In fact, there may also appear phenomena which even question the ordinal scale level. For example, in a set of items A,B,C rated with a Likert scale circular relations like A>B, B>C and C>A can appear. This violates the axiom of transitivity for the ordinal scale.
Rasch model
Likert scale data can, in principle, be used as a basis for obtaining interval level estimates on a continuum by applying the polytomous Rasch model, when data can be obtained that fit this model. In addition, the polytomous Rasch model permits testing of the hypothesis that the statements reflect increasing levels of an attitude or trait, as intended. For example, application of the model often indicates that the neutral category does not represent a level of attitude or trait between the disagree and agree categories.
Again, not every set of Likert scaled items can be used for Rasch measurement. The data has to be thoroughly checked to fulfill the strict formal axioms of the model.
Pronunciation
Rensis Likert, the developer of the scale, pronounced his name 'lick-urt' with a short "i" sound.[5][6] It has been claimed that Likert's name "is among the most mispronounced in [the] field."[7] Although many people use the long "i" variant ('lie-kurt'), those who attempt to stay true to Dr. Likert's pronunciation use the short "i" pronunciation ('lick-urt').
From Wikipedia, the free encyclopedia
The Likert scale is commonly used in survey research. It is often used to measure respondents' attitudes by asking the extent to which they agree or disagree with a particular question or statement. A typical scale might be "strongly agree, agree, not sure/undecided, disagree, strongly disagree." On the surface, survey data using the Likert scale may seem easy to analyze, but there are important issues for a data analyst to consider.
Instructions
1. Get your data ready for analysis by coding the responses. For example, let's say you have a survey that asks respondents whether they agree or disagree with a set of positions in a political party's platform. Each position is one survey question, and the scale uses the following responses: Strongly agree, agree, neutral, disagree, strongly disagree. In this example, we'll code the responses accordingly: Strongly disagree = 1, disagree = 2, neutral = 3, agree = 4, strongly agree = 5.
2. Remember to differentiate between ordinal and interval data, as the two types require different analytical approaches. If the data are ordinal, we can say that one score is higher than another. We cannot say how much higher, as we can with interval data, which tell you the distance between two points. Here is the pitfall with the Likert scale: many researchers will treat it as an interval scale. This assumes that the differences between each response are equal in distance. The truth is that the Likert scale does not tell us that. In our example here, it only tells us that the people with higher-numbered responses are more in agreement with the party's positions than those with the lower-numbered responses.
3. Begin analyzing your Likert scale data with descriptive statistics. Although it may be tempting, resist the urge to take the numeric responses and compute a mean. Adding a response of "strongly agree" (5) to two responses of "disagree" (2) would give us a mean of 4, but what is the significance of that number? Fortunately, there are other measures of central tendency we can use besides the mean. With Likert scale data, the best measure to use is the mode, or the most frequent response. This makes the survey results much easier for the analyst (not to mention the audience for your presentation or report) to interpret. You also can display the distribution of responses (percentages that agree, disagree, etc.) in a graphic, such as a bar chart, with one bar for each response category.
4. Proceed next to inferential techniques, which test hypotheses posed by researchers. There are many approaches available, and the best one depends on the nature of your study and the questions you are trying to answer. A popular approach is to analyze responses using analysis of variance techniques, such as the Mann Whitney or Kruskal Wallis test. Suppose in our example we wanted to analyze responses to questions on foreign policy positions with ethnicity as the independent variable. Let's say our data includes responses from Anglo, African-American, and Hispanic respondents, so we could analyze responses among the three groups of respondents using the Kruskal Wallis test of variance.
5. Simplify your survey data further by combining the four response categories (e.g., strongly agree, agree, disagree, strongly disagree) into two nominal categories, such as agree/disagree, accept/reject, etc.). This offers other analysis possibilities. The chi square test is one approach for analyzing the data in this way.
Read more: How to Use the Likert Scale in Statistical Analysis | eHow.com http://www.ehow.com/how_4855078_use-likert-scale-statistical-analysis.html#ixzz1LGrJsRUS
Opinion:
There's a huge debate ongoing in the social / behavioral sciences over whether Likert scales should be treated as ordinal or interval.
Count me as one who thinks it's OK to treat them as interval.
I would analyze the data both ways - with chi-square and with ANOVA, and see how it turns out - if the outcomes are the same, you're all set. If you get something different with each method, then you have something interesting...
Overall, you can treat the scales as interval and run methods that compare means, such as ANOVA. The scales are close enough to interval so that these methods shouldn't lead you astray.
Yes, Tukey would be fine for a post-hoc test. It's "middle-of-the-road" in terms of liberal/conservative (Fisher's LSD is liberal, Bonferroni is conservative).
In terms of how you would use chi-square, you could set up a comparison between the groups you want to contrast, and do the analysis on the frequency of each choice, between the groups (i.e., did one group choose "agree" more often than another group). Yes, it would be a chi-square test of independence. The contingency table could be set up with groups as rows, and scale items as 8 columns. The cells of the table would contain the response frequencies.
For chi-square post-hoc, use a simple comparison of two independent proportions with a z test.
You wouldn't necessarily report means with a chi-square analysis, since your interest is in comparing frequencies, but that's not to say you wouldn't do some sort of basic descriptive statistics comparison (means, medians, std dev, etc.)











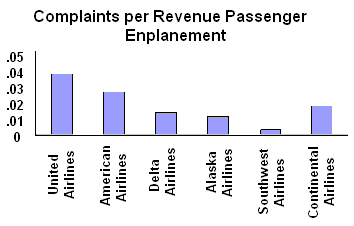
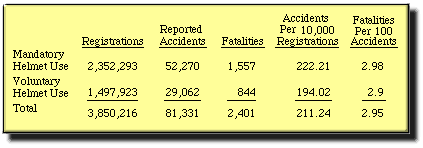

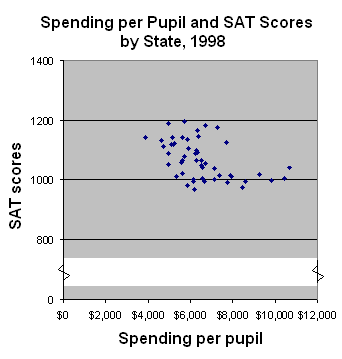
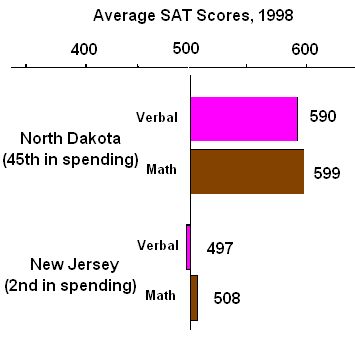






- It’s pseudomathematics. It dresses up as a concise set of theories and methods, when these would more properly be referred to as cookbooks.
- It’s simplistic. It gives a false sense of understanding about complex systems where no understanding exists. It prevents people from searching for mechanistic explanations that could indeed provide valuable insights.
- It’s self-adulatory. Its practitioners have the courage to call every little possible way to plot data a “tool” or a “method”.
- It’s too widespread. Most college programs that lack the most basic mathematics have their statistics courses (humanities and sciences), which helps spread misconceptions and misuse.
(http://flowingdata.com)
I'm cycling between extreme bouts of sleepiness and horrible anxiety about my exam, which is in 4 hours (holy fuck, how did time go by so fast?!?!) I need to make a 66 on the final to pass. Please cross your fingers, say prayers, or what ever thing you do for good luck. I have to pass this class to graduate and it is my next to last final. OK, must study more now. More info to CRAM into my exhausted brain.
(http://www.atforumz.com)
And that is why I hate statistics.
(http://blogs.poz.com)
Deb
I agree that most people think the field should be renamed "sadistics" but I am not 100% sure why it's so despised.
(http://www.stat.columbia.edu)
I bore two boys, raised them, I have undergone open heart surgery and I have NEVER experienced the level of frustration and pain as I have had in this statistics class.
The textbook is POORLY written and the online venue? DON’T have anything to do with Pearson!
I would rather eat glass, drive a pencil through my eye AND walk on coals then to put up with this crap.
There has been nothing my whole life, that could not be figured out by using just addtion, subtraction, multiplying and dividing. The plus? No STUPID rules, that if this happens, then use this or if there is this do this. PLAAEEEEZE! Who thought this junk up????
(http://flowingdata.com)
- My intro professor was without a doubt the worst professor I have ever had. This was essentially intro to statistics for non-statisticians and she took powerpoint slides right from the textbook and threw them up on a screen. Needless to say, it was absolutely useless. Then, during the lab session, she was trying to teach us R without giving us a good background on the concepts. Thankfully, I found a book that barely got me through the class and gave me a great appreciation for some of the concepts. The worst professors are those who lecture for 90 minutes, then say “Any questions.” At which point you don’t even know where to start because s/he lost you in minute two and didn’t care. This was stats for me.
(http://flowingdata.com)
(http://thedeskinthecorner.blogspot.com)
It does really stink though. It's confusing to me. Maybe taking it online was not a good idea. it might hve made more sense if I had a teacher lecturing on the material.
(http://allnurses.com)
I don’t think the uncertainty is the reason, or the order it imposes.
I think the major reason people dislike statistics is that it was poorly taught in whatever classes they took. Perhaps the instructor didn’t get it, or didn’t do the examples well.
A related reason that people don’t like statistics is that any examples they ever saw were not relevant to something they understood or cared about.
I wasn’t wild about the classroom statistics I had, but what I’ve learned since then has been interesting.
(http://flowingdata.com)
So, why do you think you should love statistics? :D